
How tall is the Great Pyramid?
This is the second episode of the Greek mathematicians series. Today’s mathematician’s name is Thales. He is also a philosopher and astronomer. He is considered “the first” Greek philosopher and is sometimes referred to as the Father of Science.
After the introduction, I started to tell my son the story of Thales. “Thales loved travelling. One day he travelled to Egypt, and visited the Great Pyramid of Khufu. For thousands of years, this was the tallest and widest building on earth. So naturally, he asked the Egyptians, how tall is the Great Pyramid?”
“Did they know?”
“It turned out everybody knew the great pyramid was tall, they just didn’t know how tall exactly.”
“So measure it! Use a ruler or something.” Son suggested.
“Well, it was easier said than done. First, the pyramid was sacred, so the Egyptians did not want people to climb on it. In fact, they painted slippery coverings on the pyramid to prevent people from climbing. Second, even if you climbed on top of it, it still would be a problem to measure the height. For measuring the height, you needed access to the top as well as the center of the bottom at the same time, which would not be possible.”
“So what did Thales do?”
“He measured the shadow of the Great Pyramid instead.”
“That’s clever! But the shadow changes right?”
“Good point. What Thales did was that he used a stick and pushed it into the ground so it standed up.”
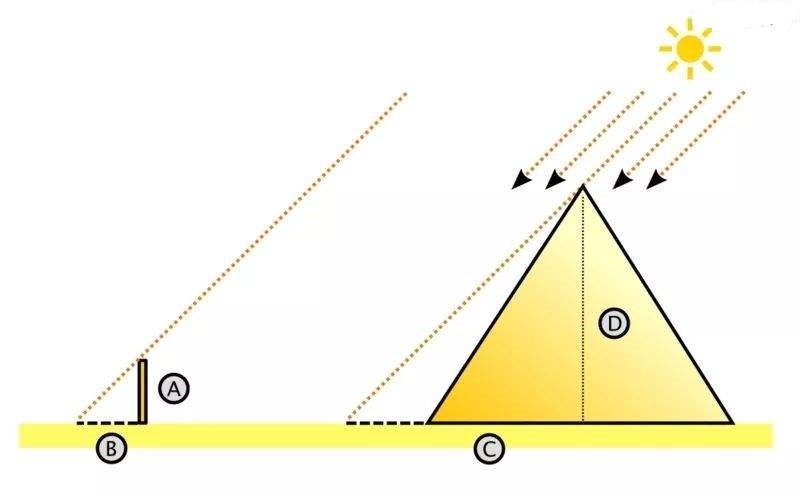
“Since the stick and the pyramid were casting shadows at the same time under the sun, the ratio of the shadow to the object was the same. So we have:”
Length(stick shadow)/Length(stick) = Length(pyramid shadow)/Length(pyramid)
“Thales used the simplest case of this equation. He waited till the shadow of the stick reached the same length of the stick. Then he measured the shadow of the pyramid, which was equal to the height of the great pyramid.”
By the way, today the Khufu pyramid is 138.5 meters (454.4 ft) tall. It actually is shorter than before, when it was once 146.5 meters (481 feet) tall.