
The Tower of Hanoi
Another fun story today!
Legend has it that, on a pouring day in the nineteenth century, a French explorer entered a giant, splendid temple in Hanoi, the capital city of Vietnam. He saw three massive pillars. 64 golden disks stacked neatly on the pillars. Monks were busy moving the disks from one pillar to another.
The monks told the explorer that they had been moving the disks for centuries. The 64 disks were originally stacked on one pillar. Each disk rested on a slightly larger disk. The goal is to move all 64 disks to another pillar, with the order preserved.
The monks needed to follow the following rules:
- Only one disk could be moved at one time.
- No disk could be placed on a smaller disk.
I am sure if you were the French explorer, you would ask the monks the same question: what would happen when the goal was achieved?
“The world will come to an end!” Said the monks.
Now that I got you to worry about the fate of the world, let’s see what the Tower of Hanoi looks like.

There are many Tower of Hanoi toys for sale these days. They are similar to the giant pillars and disks described in the story, except there are usually less than 10 disks, compared to 64 in the story. You will know why after you complete reading my article.
I bought the Tower of Hanoi toy and played with it with my son. For the first game, we used only 4 disks. Son tried to follow the rules and made some progress, but he often got distracted and tracked backwards.
“OK, it seems you are a little stuck. Let me give you a very common and useful idea. The idea applies to math problems as well as real world problems. When you are trying to solve a difficult problem, you can start with a simpler problem. For example, here we have 4 disks. Let’s start with 3 disks.” I gave my son some hints.
Son came up with the solution for 3 disks. It took 7 moves.
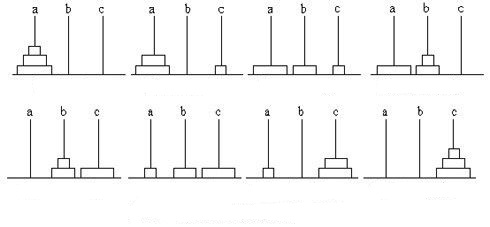
“Cool, Now let’s try 4 disks.” I asked him to continue.
“Since we cannot put a disk on top of a smaller disk, to move the largest disk from post A to another post, we need to move the top 3 disks to the third post first.” Son drew a conclusion after several rounds of discussions with me.
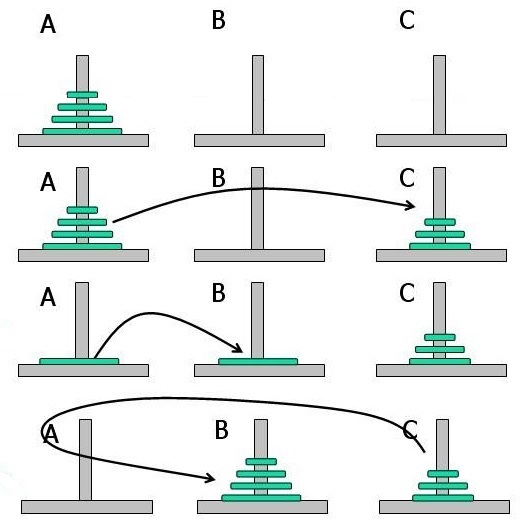
“That’s an excellent observation! AND we already knew how to move 3 disks! So the problem to move 4 disks can be broken down to three steps:
Step 1: Move the top 3 disks from A to C, that takes 7 moves.
Step 2: Move the largest disk from A to B, one move.
Step 3: Move the top 3 disks from C to B, again 7 moves.
That is 15 moves total.” I concluded.
Mathematically, we can prove that to move N disks from one post to another, it takes 2^N -1 moves. Back to the story of the Tower of Hanoi: to move 64 disks, it takes 2^64 -1 moves. That is 18,446,744,073,709,551,615 or 18 quintillion. Even if moving one disk takes 1 second, which is unlikely given how large the disk is, it will take 500 billion years to complete the task. That’s more than 10 times the age of the earth!
By the way, does this 18 quintillion number sound familiar? Right, we have encountered it in our previous story Rice on the chessboard!
Also I want to call out the thought approach we took in solving the Tower of Hanoi puzzle: To solve a complex problem, start with a simpler problem. You will find it extremely useful in solving math problems and real life problems.
I like the way you tell math stories. Very fun!